PERBAIKAN PADA APLIKASI

PERBAIKAN PADA APLIKASI SISTEM PENDETEKSI BANJIR DENGAN METODE MAMDANI DI JAKARTA

[KEMBALI KE MENU SEBELUMNYA]

DAFTAR ISI

1. Tujuan

2. Alat dan Bahan

3.Dasar Teori

example

problem

pilihan ganda

4.Langkah percobaan

5. Video Pengenalan Fuzzy dengan Matlab

6. Link Download 

1. Tujuan [Back]

Mengetahui toolbox yang terdapat pada Matlab

Mampu memahami cara kerja dari toolbox yang terdapat dari Matlab

           Dapat menjalankan program dengan menggunakan Matlab

    

2. Alat dan Bahan[Back]

  Alat yang digunakan yaitu Software Matlab.

Buku Fuzzy

Agus, Naba. (2009). "Belajar cepat Fuzzy Logic Menggunakan Matlab".C.V Andi Offset, Yogyakarta, 

3. Dasar Teori [Back]

A. Pengenalan Fuzzy Logic

        Logika Fuzzy merupakan suatu logika yang memiliki nilai kekaburan atau kesamaran (fuzzyness) antara benar atau salah.Logika fuzzy dapat digunakan dalam bidang teori kontrol, teori keputusan, dan beberapa bagian dalam managemen sains. 

        Kelebihan dari logika fuzzy adalah mampu dalam proses penalaran secara bahasa (linguistic reasoning), sehingga dalam perancangannya tidak perlu lagi persamaan matematik dari objek yang dikendalikan. 

        Adapun salah satu contoh dari aplikasi logika fuzzy dalam kehidupan sehari-hari adalah di tahun 1990 pertama kali dibuat mesin cuci dengan logika fuzzy di Jepang (Matsushita Electric Industrial Company). 

        Sistem fuzzy digunakan untuk menentukan putaran yang tepat secara otomatis berdasarkan jenis dan banyaknya kotoran serta jumlah yang akan dicuci

Operasi Himpunan Fuzzy

Operasi himpunan kabur diperlukan untuk proses inferensi atau penalaran. Dalam hal ini yang dioperasikan adalah derajat keanggotannya. Derajat keanggotaannya sebagai hasil dari operasi dua buah himpunan kabur. ada 3 operator dasar yang terdapat dalam himpunan Fuzzy, yaitu operator AND, operator OR dan operator NOT .

1. Operator and (konjungsi) fuzzy

Kongjungsi fuzzy dari A dan B dilambangkan dengan  A n B   dan didefenisikan oleh :

contoh.
A ∩ B = {MIN(1.0, 0.2), MIN(0.20, 0.45), MIN(0.75, 0.50)} = {0.2, 0.20, 0.50}
Misal nilai keanggotaan umur 27 pada himpunan muda adalah μMUDA[27] = 0,6 dan nilai keanggotaan 2 juta pada himpunan penghasilan TINGGI adalah μGAJITINGGI[2juta] = 0,8

maka α -predikat untuk usia MUDA dan berpenghasilan TINGGI adalah nilai

keanggotaan minimun :

μMUDA ∩ GAJITINGGI

= min(μ MUDA[27], μ GAJITINGGI[2juta])

= min (0,6 ;  0,8)

= 0,6

2. Operator OR (disjungsi) fuzzy

Disjungsi fuzzy dari A dan B dilambangkan dengan A U B    dan didefenisikan oleh :

Contoh:

A = {1.0, 0.20, 0.75}

B = {0.2, 0.45, 0.50}

A ∪ B = {MAX(1.0, 0.2), MAX(0.20, 0.45), MAX(0.75, 0.50)}

= {1.0, 0.45, 0.75}

Misal nilai keanggotaan umur 27 pada himpunan muda adalah μMUDA[27] = 0,6 dan nilai keanggotaan 2 juta pada himpunan penghasilan TINGGI adalah μGAJITINGGI[2juta] = 0,8

maka α -predikat untuk usia MUDA atau berpenghasilan TINGGI adalah nilai keanggotaan maksimum :
μMUDA ∪ GAJITINGGI

= max(MUDA[27], GAJITINGGI[2juta])
= max (0,6 ;  0,8)
= 0,8

3. Operator NOT

range derajat keanggotaan dalam interval tertutup antara 0 dan 1, disebut complemen

dari himpunan fuzzy yang bersesuaian dengan himpunan

universal X dinotasikan  dan didefenisikan :

Contoh
Ac = {1 – 1.0, 1 – 0.2, 1 – 0.75} = {0.0, 0.8, 0.25}
Misal nilai keanggotaan umur 27 pada himpunan muda adalah μMUDA[27]= 0,6   maka α -predikat untuk usia TIDAK MUDA adalah :

μMUDA’[27]  = 1 - MUDA[27
         = 1 - 0,6
         = 0,4

Contoh Nilai keanggotaan sebagai hasil dari operasi 2 himpunan: fire strength  atau α-predikat

Fungsi Keanggotan Fungsi keanggotaan (membership function) adalah suatu kurva yang menunjukkan pemetaan titik-titik input data ke dalam nilai keanggotannya (sering juga disebut dengan derajat keanggotaan) yang memiliki interval antara 0 sampai 1. Salah satu cara yang dapat digunakan untuk mendapatkan nilai keanggotaan adalah dengan melalui pendekatan fungsi dengan u[X]  adalah derajat keanggotaan. Derajat keanggotaan yaitu nilai-nilai yang terdapat pada variabel linguistik yang dipetakan ke interval [0,1 ]. Nilai pemetaan inilah yang disebut sebagai nilai keanggotaan atau derajat keanggotaan.

B. Konsep Dasar Fuzzy Logic

Konsep Dasar  

• Logika fuzzy bukanlah logika yang tidak jelas (kabur),  tetapi logika yang digunakan untuk menggambarkan ketidakjelasan. 
• Logika fuzzy adalah teori himpunan fuzzy  Himpunan yang mengkalibrasi ketidakjelasan. 
• Logika fuzzy didasarkan pada gagasan bahwa segala sesuatu mempunyai nilai derajat. 
• Logika fuzzy merupakan peningkatan dari logika Boolean yang mengenalkan konsep kebenaran sebagian.
• Logika klasik (Crisp Logic) menyatakan bahwa segala hal dapat diekspresikan dalam istilah binary (0 atau 1, hitam atau putih, ya atau tidak) Tidak ada nilai diantaranya 2. Logika fuzzy menggantikan kebenaran boolean dengan tingkat kebenaran Ada nilai diantara hitam dan putih (abu-abu).

        C. Meteodologi Desain Fuzzy Logic

Ada tiga proses utama jika ingin mengimplementasikan fuzzy logic pada suatu perangkat, yaitu fuzzifikasi, evaluasi rule, dan defuzzifikasi.

• Fuzzifikasi = proses untuk mengubah suatu masukan dari bentuk tegas (crisp) menjadi fuzzy yang biasanya disajikan dalam bentuk himpunan-himpunan fuzzy dengan suatu fungsi kenggotaannya masing-masing.
• Interference System (Evaluasi Rule) = sebagai acuan untuk menjelaskan hubungan antara variable-variabel masukan dan keluaran yang mana variabel yang diproses dan yang dihasilkan berbentuk fuzzy.
• Defuzzification = proses pengubahan variabel berbentuk fuzzy tersebut menjadi data-data pasti (crisp) yang dapat dikirimkan ke peralatan pengendalian. 

Untuk melakukan perancangan suatu sistem fuzzy perlu dilakukan beberapa tahapan berikut ini :

1.  Mendefinisikan karakteristik model secara fungsional dan operasional.

2. Melakukan dekomposisi variabel model menjadi himpunan fuzzy

3. Membuat aturan fuzzy

4. Menentukan metode defuzzy untuk tiap-tiap variabel solusi

Berikut diagram alir prosesnya :

D. Contoh Penyelesaian Fuzzy Logic

Contoh: S = {1, 2, 3, 4, 5} adalah semesta pembicaraan A = {1, 2, 3} dan B = {3, 4, 5}  Bisa dikatakan bahwa:

Example [Back]

1. Apa itu pernyataan for ?

Jawab :

Pernyataan Loop FOR mengeksekusi group perintah secara berulang-ulang dengan jumlah iterasi yang tetap (fixed), for harus diakhiri dengan end

2. Apa itu pernyataan while?

Jawab:

Pernyataan loop while mengeksekusi group perintah secara berulang dengan jumlah iterasi yang indefinite yang ditentukan oleh suatu kondisi atau ekspresi logika tertentu. Pernyataan while harus diakhiri dengan end

Problem [Back]

1. Buatlah program yang meminta input angka sebanyak N, dimana N adalah input dari pengguna. Output program adalah bilangan maksimum dan minimum dari angka-angka tersebut.

jumlah = input(‘masukkan bilangan ke-n: ‘);
Vektor = [];

for i=1:jumlah
n = input(‘masukkan angka: ‘);
Vektor = [Vektor n];
end

maksimal = max(Vektor);
minimal = min(Vektor);

disp([‘max= ‘ num2str(maksimal)]);
disp([‘min= ‘ num2str(minimal)]);

2.Buatlah program yang bisa menyimpan input berupa bilangan-bilangan integer ke dalam array. Lalu, dari bilangan-bilangan tersebut akan muncul bilangan-bilangan yang habis dibagi 4.

j = 0;
x = input(‘masukkan x dalam bentuk [array]: ‘);
panjang = length(x);

for i = 1:panjang

sisa = mod(x(i),4);

if(sisa == 0)
j = j+1;
y(j)= x(i);
end
end

disp(y(1:j));

Pilihan Ganda[Back]

1. Berikut ini yang merupakan fungsi untuk membuat plot 3D ialah....

A. For

B. If

C. Mesh

D. While

E. Switch

2. Berikut ini yang bukan merupakan fungsi flow control ialah....

A. For

B. If

C. Break

D. While

E. Surf

4.Langkah percobaan [Back]

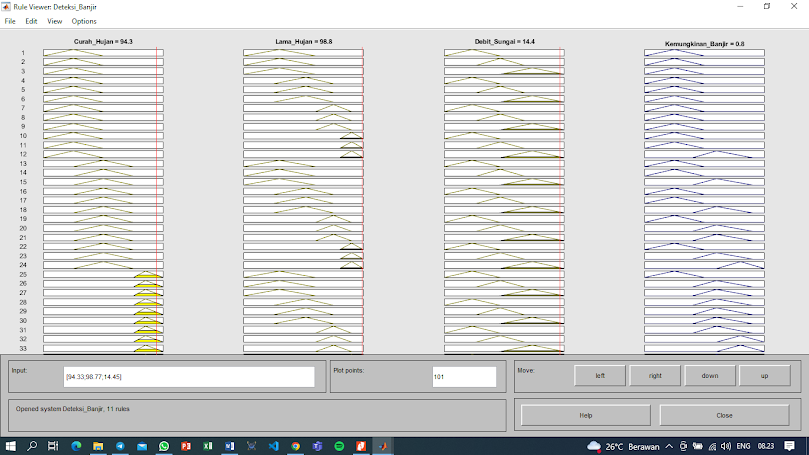
Penelitian menggunakan Fuzzy inference system (FIS)ini terdiri dari tiga variable input dan satu variable output. Variable input terdiri dari Curah hujan, Lama hujan, dan Debit sungai. Dan variable output yakni Kemungkinan banjir.

INPUT 1
Curah Hujan	Keterangan
Tidak Hujan	0 – 5 mm/hari
Sangat Rendah	0 – 28 mm/hari
Rendah	16 – 44 mm/hari
Menengah	33 – 55 mm/hari
Cukup Tinggi	50 - 86 mm / hari
Tinggi	68 – 96 mm/hari
Sangat Tinggi	88 -100 mm/hari

INPUT 2
Lama Hujan	Keterangan
Tidak hujan	0 – 4 menit
Sangat Sebentar	4 – 18 menit
Sebentar	9 – 28 menit
Sedang	25 – 60 menit
Cukup lama	40 – 70 menit
Lama	70 – 88 menit
Sangat lama	86 - 100 menit

INPUT 3
Debit Sungai	Keterangan
Tidak ada	0 - 2 m3/s
Sangat Rendah	1 -3 m3/s
Rendah	3 – 6 m3/s
Sedang	4 – 9 m3/s
Cukup Tinggi	8 – 11 m3/s
Tinggi	9 - 13 m3/s
Sangat Tinggi	12 - 15 m3/s

Output

Tidak Banjir

Banjir Sangat Kecil

Banjir Kecil

Banjir sedang

Banjir cukup besar

Banjir besar

Banjir sangat besar

A. Proses Inferensi

NO	INPUT			Output
	Curah Hujan	Lama Hujan	Debit Sungai	Prediksi Banjir
1	Gerimis	Sebentar	Rendah	Tidak banjir
2	Gerimis	Sebentar	Sedang	Tidak banjir
3	Gerimis	Sebentar	Tinggi	Tidak banjir
4	Gerimis	Sedang	Rendah	Tidak banjir
5	Gerimis	Sedang	Sedang	Tidak Banjir
6	Gerimis	Sedang	Tinggi	Tidak banjir
7	Gerimis	Lama	Rendah	Tidak Banjir
8	Gerimis	Lama	Sedang	Tidak Banjir
9	Gerimis	Lama	Tinggi	Tidak Banjir
10	Gerimis	Sangat Lama	Rendah	Tidak Banjir
11	Gerimis	Sangat lama	Sedang	Tidak banjir
12	Gerimis	Sangat lama	Tinggi	Banjir Sedang
13	Sedang	Sebentar	Rendah	Tidak Banjir
14	Sedang	Sebentar	Sedang	Tidak banjir
15	Sedang	Sebentar	Tinggi	Banjir Sedang
16	Sedang	Sedang	Rendah	Tidak Banjir
17	Sedang	Sedang	Sedang	Tidak Banjir
18	Sedang	Sedang	Tinggi	Banjir Sedang
19	Sedang	Lama	Rendah	Tidak banjir
20	Sedang	Lama	Sedang	Banjir sedang
21	Sedang	Lama	Tinggi	Banjir sedang
22	Sedang	Sangat lama	Rendah	Tidak Banjir
23	Sedang	Sangat lama	Sedang	Banjir sedang
24	Sedang	Sangat lama	Tinggi	Banjir besar
25	Deras	Sebentar	Rendah	Tidak Banjir
26	Deras	Sebentar	Sedang	Banjir sedang
27	Deras	Sebentar	Tinggi	Banjir Sedang
28	Deras	Sedang	Rendah	Banjir Sedang
29	Deras	Sedang	Sedang	Banjir sedang
30	Deras	Sedang	Tinggi	Banjir Sedang
31	Deras	Lama	Rendah	Banjir Sedang
32	Deras	Lama	Sedang	Banjir Besar
33	Deras	Lama	Tinggi	Banjir Besar
34	Deras	Sangat lama	Rendah	Banjir Sedang
35	Deras	Sangat lama	Sedang	Banjir Besar
36	Deras	Sangat lama	Tinggi	Banjir besar

B. Implementasi Sistem Pada Matlab dan  Defuzzyfikasi

0. Ketikkan Fuzzy di Command Window

1. Desain Fuzzy Logic membuat input dan output 

Mamdani pada aplikasi Matlab. 

2. Variabel input nilai pada curah hujan dengan nilai  input pada Gerimis : 0 25 50; Sedang : 25 50 75; Deras : 75  85 100; 

3.  Variabel input pada lama hujan dengan nilai input  Sebentar : 0 30 60; Sedang : 25 52 75; Lama : 60 75 90; Sangat Lama : 80 90 100; 

4.  Variabel input pada Debit sungai dengan nilai input Rendah : 0 3.5 7; Sedang : 4 7 10; Tinggi : 7 11 15; 

5. Variabel output Kemungkinan banjir dengan input  nilai Tidak Banjir : 0 0.25 0.5; Banjir Sedang : 0.4 0.6 0.9; Banjir Besar : 0.6 0.8 1; 

6. Masukkan Rules

7. Rule Viewer Mamdani proses dari Matlab Deteksi Banjir

5. Video Pengenalan Fuzzy dengan Matlab[Back]

Video Referensi Penerapan Fuzzy pada pendeteksi Banjir

Video Perbaikan Aplikasi

6. Link Download[Back]

• Download File HTML [klik disini]
• Download Video Penjelasan  [klik disini]
• Download Codingan [klik disini]
• Download Jurnal [klik disini]